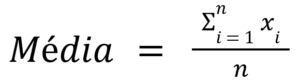Como referenciar este texto: ‘Entendendo medidas de tendência central: Média, Mediana e Moda’. Rodrigo Terra. Publicado em: 03/01/2025. Link da postagem: https://www.makerzine.com.br/dados/entendendo-medidas-de-tendencia-central-media-mediana-e-moda/.
Conteúdos que você verá nesta postagem
As medidas de tendência central são ferramentas estatísticas fundamentais para a análise de dados, usadas para resumir um conjunto de valores em um único número que representa seu “centro” ou “ponto de equilíbrio”. Entre as mais comuns estão a média, a mediana e a moda, cada uma com características específicas que atendem a diferentes necessidades de interpretação.
Essas medidas são cruciais na análise de dados porque permitem extrair informações relevantes de grandes volumes de dados. Por meio delas, é possível identificar padrões, tendências e comportamentos gerais de um conjunto de informações, auxiliando na simplificação e interpretação de dados complexos. Por exemplo, uma empresa pode usar a média para calcular o desempenho médio de seus produtos, a mediana para avaliar a faixa salarial mais representativa de seus colaboradores e a moda para entender qual produto tem a maior preferência entre os clientes.
No mundo atual, em que a tomada de decisões baseia-se cada vez mais em dados, as medidas de tendência central desempenham um papel estratégico em diversas áreas. Em negócios, elas ajudam na definição de preços e estratégias de mercado. Na saúde, permitem análises como a idade média de pacientes diagnosticados com uma condição específica ou a mediana do tempo de espera em emergências hospitalares. Já na tecnologia, são empregadas para avaliar o comportamento dos usuários em plataformas digitais, identificando padrões de uso e preferências.
Média Aritmética: A Primeira Referência
A média aritmética é a medida de tendência central mais conhecida e amplamente utilizada. Ela é definida como a soma de todos os valores de um conjunto dividida pelo número total de elementos nesse conjunto. Em termos simples, a média representa um ponto de equilíbrio, fornecendo uma visão geral do comportamento dos dados.
No contexto de dados, a média é frequentemente utilizada para sintetizar informações e oferecer uma primeira interpretação do conjunto analisado. Por exemplo, em uma empresa, o cálculo da média mensal de vendas pode ajudar a identificar tendências de crescimento ou retração, servindo como um indicador inicial de desempenho.
Como calcular a média aritmética
Calculamos a média aritmética seguindo a equação abaixo:
Onde:
- xi são os valores individuais do conjunto de dados.
- n é o número total de valores no conjunto.
Exemplo de aplicação
Imagine uma empresa que registra suas vendas semanais em um mês:
100, 150, 200, 250
Para calcular a média, somamos os valores:
100+150+200+250=700
Dividimos pelo número total de semanas (n=4):
Média=700 / 4 = 175
A média semanal de vendas é 175 unidades, o que fornece uma visão inicial do desempenho durante o mês.
Como interpretar a média artimética
- Contexto homogêneo: A média funciona bem quando os valores estão próximos entre si, oferecendo uma visão precisa do centro dos dados.
- Dados com outliers: Em casos de valores extremos (outliers), a média pode ser distorcida, não representando adequadamente o conjunto. Por exemplo, em uma análise salarial, a presença de um salário muito alto pode elevar a média, tornando-a pouco representativa para a maioria dos trabalhadores.
Mediana: O Valor Central
A mediana é uma medida de tendência central que identifica o valor central de um conjunto de dados ordenado. Diferentemente da média, a mediana não é influenciada por valores extremos (outliers), o que a torna especialmente útil em conjuntos de dados assimétricos ou com grande variabilidade.
Definição e Papel em Datasets Assimétricos
A mediana é definida como o valor que separa a metade inferior da metade superior de um conjunto de dados ordenado. Em conjuntos com um número ímpar de elementos, a mediana é o valor central. Em conjuntos com um número par de elementos, a mediana é a média aritmética dos dois valores centrais.
No contexto de dados assimétricos, a mediana é crucial porque oferece uma representação mais robusta e confiável do comportamento típico dos dados, especialmente em situações onde valores extremos podem distorcer a média. Por exemplo, em análises de renda, o uso da mediana é preferível para evitar que salários muito altos influenciem desproporcionalmente o resultado.
Exemplo prático: Análise do preço mediano de imóveis
Imagine que uma imobiliária esteja analisando os preços de casas em uma cidade. Os valores registrados são:
200.000, 220.000, 250.000, 1.000.000, 1.500.000
- Primeiro, ordenamos os dados (já estão em ordem).
- Identificamos o valor central: 250.000.
Nesse caso, a mediana (250.000) representa melhor o mercado típico de imóveis do que a média:
Média = (200.000 + 220.000 + 250.000 + 1.000.000 + 1.500.000) / 5
Média = 634.000
O valor médio é muito mais alto devido à influência dos imóveis de alto valor, enquanto a mediana reflete o preço mais comum na faixa intermediária.
Comparação com a média em situações com dados extremos
A diferença entre a média e a mediana é mais evidente em situações com valores extremos. A média, ao considerar todos os valores, é sensível a outliers, o que pode resultar em uma interpretação distorcida dos dados. Já a mediana, ao focar apenas no valor central, é menos suscetível a essas distorções.
Por exemplo:
- Em um dataset de rendimentos mensais, onde a maioria das pessoas ganha entre 2.000 e 3.000, mas um executivo recebe 100.000, a mediana reflete melhor a realidade do grupo.
- Em análises de mercado imobiliário, a mediana é preferida porque grandes propriedades de luxo podem elevar a média sem representar o mercado típico.
A mediana é, portanto, uma medida indispensável para interpretar dados assimétricos ou quando a presença de valores extremos pode comprometer a análise.
Como interpretar a mediana
- Contextos assimétricos: A mediana é ideal para representar conjuntos de dados com outliers, pois esses valores não afetam sua posição.
- Distribuição equilibrada: Em conjuntos simétricos, a mediana e a média geralmente coincidem, reforçando sua interpretação como o valor central.
Moda: A frequência importa
A moda é a medida de tendência central que identifica o valor ou categoria mais frequente em um conjunto de dados. Ela é especialmente útil para analisar dados categóricos ou em situações em que a frequência é o foco principal da análise. Ao contrário da média e da mediana, a moda não depende de cálculos aritméticos, mas sim da contagem de ocorrências.
Definição e uso em dados categóricos
A moda é o elemento que ocorre com maior frequência em um conjunto de dados. Em dados categóricos, onde os valores representam categorias ou rótulos, a moda se destaca como a única medida de tendência central aplicável. Por exemplo, ao analisar a preferência de consumidores por cores de um produto, a moda ajuda a identificar a cor mais escolhida.
Além disso, a moda pode ser aplicada em dados quantitativos, especialmente quando se busca identificar valores recorrentes, como o número mais frequente de visitas a uma loja ou a nota mais comum de uma prova.
Exemplo: Identificação de categorias de produtos mais vendidos
Imagine uma loja de roupas que registra as vendas de diferentes tamanhos de camisetas em uma semana:
Tamanhos vendidos: P, M, M, G, M, GG, P, M, M, GG
Contamos a frequência de cada tamanho:
- P: 2
- M: 5
- G: 1
- GG: 2
O tamanho com maior frequência é M, que foi vendido 5 vezes.
Nesse caso, a moda é o tamanho M, indicando que ele é o mais procurado pelos clientes. Essa informação pode ser usada para ajustar estoques e atender à demanda com maior eficiência.
Aplicações em ciência de dados: Análise de preferências de usuários
A moda é amplamente utilizada em ciência de dados para análises baseadas em comportamento de usuários e preferências. Algumas aplicações incluem:
- Recomendações de produtos: Identificar os itens mais comprados por um grupo de clientes para oferecer sugestões personalizadas.
- Análise de palavras-chave: Encontrar as palavras ou frases mais buscadas em um site, otimizando estratégias de SEO.
- Interação com sistemas digitais: Determinar a funcionalidade mais utilizada em uma plataforma, auxiliando na priorização de melhorias no design.
Por exemplo, em uma plataforma de streaming, a moda pode ser usada para identificar o gênero de filme mais assistido por usuários em um determinado período, ajudando na curadoria de conteúdo personalizado.
Como interpretar a moda
- Dados categóricos: A moda é a única medida de tendência central aplicável, como em preferências de clientes, categorias de produtos ou respostas em uma pesquisa.
- Dados numéricos: Em casos com múltiplas modas (bimodal ou multimodal), ela pode indicar grupos distintos dentro do conjunto de dados.
Interpretação no Contexto de Dados
As medidas de tendência central são ferramentas essenciais para transformar conjuntos de dados complexos em informações compreensíveis e acionáveis. Elas ajudam a resumir os dados de forma clara, fornecendo uma visão geral que permite identificar tendências, padrões e comportamentos gerais. Essa simplicidade é fundamental para a comunicação eficaz de insights, especialmente em contextos corporativos, educacionais e tecnológicos.
Como Resumir e Comunicar Insights
Ao condensar grandes volumes de dados em métricas como média, mediana e moda, essas medidas permitem que analistas apresentem informações de forma objetiva e acessível. Por exemplo:
- A média pode indicar o desempenho médio de um departamento ou equipe.
- A mediana destaca o ponto central, especialmente útil em dados assimétricos.
- A moda identifica os elementos mais frequentes, como preferências de clientes ou padrões de uso.
Ao comunicar esses insights, o foco está em traduzir os números em histórias que facilitem a tomada de decisão. Gráficos e visualizações, como histogramas, boxplots ou gráficos de barras, complementam as medidas de tendência central, tornando os dados mais intuitivos.
Papel das Medidas de Tendência Central em Relatórios e Dashboards
Em relatórios e dashboards, as medidas de tendência central desempenham um papel crucial como indicadores-chave de desempenho (KPIs). Elas servem como referências rápidas e precisas para avaliar o estado atual de um sistema ou processo. Exemplos incluem:
- Média de vendas mensais para monitorar o desempenho do setor comercial.
- Mediana de tempos de entrega para avaliar a eficiência logística.
- Moda de interações em uma plataforma digital para priorizar melhorias no design da interface.
Relatórios baseados nessas medidas são fáceis de interpretar e ajudam stakeholders a tomar decisões fundamentadas sem necessidade de análise técnica aprofundada. Dashboards interativos, por sua vez, permitem explorar os dados em tempo real, combinando tendências centrais com outras métricas, como variações e dispersão.
Exemplo: Apresentação de KPIs para Stakeholders
Imagine um cenário em que uma empresa de e-commerce apresenta seu desempenho trimestral para os investidores. O dashboard inclui:
- Média de vendas por cliente: R$350, indicando o gasto médio de cada comprador.
- Mediana de entregas em dias: 333, destacando que a maioria dos pedidos é entregue rapidamente, apesar de alguns atrasos.
- Moda dos produtos vendidos: “Celulares”, mostrando a categoria mais popular entre os clientes.
Essas métricas permitem aos stakeholders entender rapidamente os principais resultados e direcionar perguntas específicas. Por exemplo, o foco na mediana das entregas pode levar a discussões sobre como otimizar a logística, enquanto a moda dos produtos vendidos pode orientar decisões sobre estoques e campanhas de marketing.
Se você acha que este conteúdo pode ser útil para alguém, compartilhe!
Ao divulgar os textos do MakerZine, você contribui para que todo o material continue acessível e gratuito para todas as pessoas.