Como referenciar este post: Regressão linear: Principais conceitos, tipos, limitações, aplicações e exemplo. Rodrigo R. Terra. Publicado em: 22/08/2023 Link da postagem: https://www.makerzine.com.br/cozinha-de-dados/regressao-linear-principais-conceitos-tipos-limitacoes-aplicacoes-e-exemplo.
Conteúdos dessa postagem
A regressão linear é uma técnica estatística fundamental que tem sido amplamente utilizada para modelar a relação entre variáveis em diversas áreas, desde a ciência de dados até a pesquisa científica. É uma ferramenta poderosa para fazer previsões, entender tendências e tomar decisões baseadas em dados.
Em essência, a regressão linear busca encontrar uma equação linear que melhor descreva a relação entre uma variável dependente (ou resposta) e uma ou mais variáveis independentes (ou preditores). A variável dependente é aquela que queremos prever ou explicar, enquanto as variáveis independentes são aquelas que usamos para fazer a previsão.
A forma mais simples de regressão linear é a regressão linear simples, também conhecida como univariada, que envolve apenas duas variáveis: uma variável dependente (Y) e uma variável independente (X). A relação entre essas variáveis é modelada como uma linha reta, representada pela equação:
Y = β₀ + β₁X + ε
Nesta equação, β₀ é o coeficiente de intercepção, que representa o valor de Y quando X é igual a zero. O coeficiente β₁ é o coeficiente angular, indicando como Y muda em resposta a uma mudança unitária em X. O termo ε representa o erro aleatório, que é a diferença entre os valores reais de Y e os valores previstos pela equação da regressão. O objetivo da regressão linear é encontrar os valores dos coeficientes (β₀ e β₁) que minimizem a soma dos quadrados dos resíduos (erros) e, assim, melhor ajustem a linha aos dados.
Quando há mais de uma variável independente, temos a regressão linear múltipla, também conhecida como multivariada. Nesse caso, a equação da regressão linear geral fica assim:
Y = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ + ε
Onde X₁, X₂, …, Xₚ representam as diferentes variáveis independentes e β₁, β₂, …, βₚ são os seus respectivos coeficientes.
A regressão linear é frequentemente aplicada em diversas áreas, como ciências sociais, economia, engenharia, ciências naturais, entre outras. Seu uso abrange desde análises simples, como a relação entre salário e anos de experiência, até estudos complexos que envolvem várias variáveis para explicar fenômenos complexos.
Uma das grandes vantagens da regressão linear é a facilidade de interpretação dos resultados. Os coeficientes estimados fornecem informações sobre a magnitude e direção da relação entre as variáveis, permitindo entender como uma mudança nas variáveis independentes afeta a variável dependente.
No entanto, é importante ressaltar que a regressão linear possui algumas limitações. Ela presume uma relação linear entre as variáveis e pode ser sensível a outliers e violações de seus pressupostos. Nesses casos, outras técnicas de modelagem, como regressão não linear, podem ser mais adequadas.
Conceitos básicos
A regressão linear é uma técnica estatística fundamental que nos permite entender e modelar as relações entre variáveis. Antes de mergulharmos em detalhes mais complexos, é essencial conhecer alguns conceitos básicos que fundamentam essa importante ferramenta analítica.
1. Variável Dependente e Variáveis Independentes: Na regressão linear, trabalhamos com duas categorias principais de variáveis. A variável dependente (ou variável resposta) é aquela que queremos prever ou explicar. Por exemplo, se estivermos estudando a relação entre o tempo de estudo e o desempenho acadêmico de estudantes, o desempenho acadêmico seria a variável dependente.
As variáveis independentes (ou variáveis preditoras), por outro lado, são aquelas que usamos para fazer a previsão ou explicar a variação da variável dependente. No exemplo anterior, o tempo de estudo seria uma variável independente, pois queremos entender como ela afeta o desempenho acadêmico.
2. Equação da Regressão Linear: A equação da regressão linear é a base matemática da técnica. No caso da regressão linear simples (univariada), a equação é uma linha reta representada por:
Y = β₀ + β₁X + ε
Onde:
- Y é a variável dependente que queremos prever.
- X é a variável independente que usamos para fazer a previsão.
- β₀ é o coeficiente de intercepção, que representa o valor de Y quando X é igual a zero.
- β₁ é o coeficiente angular, que indica como Y muda em resposta a uma mudança unitária em X.
- ε é o termo de erro, que representa a diferença entre os valores reais de Y e os valores previstos pela equação da regressão.
3. Coeficientes de Regressão: Os coeficientes β₀ e β₁ são estimados a partir dos dados disponíveis e desempenham um papel crítico na equação da regressão linear. O coeficiente de intercepção (β₀) determina o ponto em que a linha de regressão intercepta o eixo vertical (Y), enquanto o coeficiente angular (β₁) define a inclinação da linha.
4. Método dos Mínimos Quadrados: Para encontrar os valores ótimos dos coeficientes β₀ e β₁, utilizamos o método dos mínimos quadrados. Esse método busca minimizar a soma dos quadrados das diferenças entre os valores reais e os valores previstos pela equação da regressão. O resultado são os melhores coeficientes que ajustam a linha de regressão aos dados disponíveis.
5. Regressão Linear Múltipla: Quando temos mais de uma variável independente, utilizamos a regressão linear múltipla. Nesse caso, a equação se expande para incluir todas as variáveis independentes e seus respectivos coeficientes. A equação geral fica assim:
Y = β₀ + β₁X₁ + β₂X₂ + … + βₚXₚ + ε
A regressão linear múltipla é especialmente útil para explicar fenômenos complexos que podem ser influenciados por várias variáveis simultaneamente.
6. Interpretação dos Coeficientes: Uma das principais vantagens da regressão linear é a facilidade de interpretação dos coeficientes. Os valores estimados para β₀ e β₁ fornecem informações sobre a magnitude e direção da relação entre as variáveis. Por exemplo, um coeficiente β₁ positivo indica uma relação positiva entre a variável independente e a variável dependente.
Tipos de Regressão Linear
A regressão linear é uma ferramenta poderosa para modelar a relação entre variáveis e fazer previsões com base em dados. À medida que nossas análises se tornam mais complexas e os dados se tornam mais diversificados, diferentes tipos de regressão linear podem ser aplicados para lidar com cenários específicos. Vamos explorar alguns dos tipos mais comuns de regressão linear e entender suas aplicações.
1. Regressão Linear Simples (Univariada): A regressão linear simples é o tipo mais básico e envolve apenas duas variáveis: uma variável dependente (Y) e uma variável independente (X). A equação da regressão linear simples é uma linha reta que busca descrever a relação entre essas duas variáveis. Esse tipo de regressão é adequado quando estamos interessados em entender como uma única variável independente afeta a variável dependente.
2. Regressão Linear Múltipla (Multivariada): A regressão linear múltipla é uma extensão da regressão linear simples, permitindo que trabalhemos com mais de uma variável independente. Nesse caso, a equação da regressão inclui todas as variáveis independentes e seus respectivos coeficientes. A regressão linear múltipla é amplamente utilizada quando várias variáveis podem influenciar a variável dependente simultaneamente.
3. Regressão Linear Ponderada: A regressão linear ponderada é uma variação do método padrão de regressão linear que atribui diferentes pesos aos pontos de dados durante a análise. Isso significa que alguns pontos de dados têm mais influência na construção da linha de regressão do que outros. Essa abordagem é útil quando a heterocedasticidade está presente nos dados, ou seja, a variância dos resíduos não é constante em diferentes níveis das variáveis independentes.
4. Regressão Linear Polinomial: A regressão linear polinomial é usada quando a relação entre as variáveis parece mais complexa do que uma linha reta. Nesse tipo de regressão, os coeficientes angulares são representados por termos polinomiais, como X², X³, e assim por diante. Isso permite que a linha de regressão se ajuste melhor a padrões curvilíneos nos dados. No entanto, é preciso ter cuidado para evitar a sobreajustagem (overfitting) do modelo aos dados.
5. Regressão Linear Regularizada: A regressão linear regularizada é uma abordagem que combina a regressão linear tradicional com termos de regularização, como a regressão Ridge e a regressão Lasso. Esses termos de regularização são adicionados à função objetivo da regressão para controlar a complexidade do modelo e evitar problemas de multicolinearidade. A regressão linear regularizada é particularmente útil quando há alta colinearidade entre as variáveis independentes.
Cada tipo de regressão linear tem suas próprias vantagens e aplicações específicas. A escolha do tipo de regressão depende da natureza dos dados, dos objetivos da análise e das suposições subjacentes. Em todos os casos, a regressão linear serve como uma base sólida para modelar relacionamentos e tomar decisões informadas com base em dados observados. Ao entender esses diferentes tipos de regressão linear, podemos explorar uma ampla variedade de cenários e extrair informações valiosas para enfrentar os desafios complexos enfrentados nas mais diversas áreas de estudo e pesquisa.
Pressupostos da Regressão Linear
A regressão linear é uma técnica poderosa para modelar relações entre variáveis e fazer previsões com base em dados. No entanto, é importante lembrar que a regressão linear possui certos pressupostos que devem ser atendidos para que os resultados sejam válidos e confiáveis. Vamos explorar os principais pressupostos da regressão linear e entender sua importância na análise estatística.
1. Linearidade: O pressuposto mais fundamental da regressão linear é que a relação entre a variável dependente e as variáveis independentes é linear. Isso significa que, quando plotamos os dados em um gráfico, esperamos que a relação seja aproximadamente uma linha reta. Se a relação não for linear, a regressão linear pode não ser adequada e outras técnicas de modelagem podem ser mais apropriadas.
2. Homoscedasticidade: O pressuposto de homoscedasticidade refere-se à igualdade da variância dos erros em diferentes níveis das variáveis independentes. Em outras palavras, os resíduos (diferenças entre os valores reais e os valores previstos) devem ter uma dispersão constante ao longo da linha de regressão. Se a variância dos resíduos mudar com os valores das variáveis independentes, temos heterocedasticidade, o que pode comprometer a precisão do modelo e as inferências estatísticas.
3. Independência dos Erros: O pressuposto de independência dos erros significa que os resíduos não devem apresentar correlação entre si. Em outras palavras, não deve haver padrões ou estruturas nos resíduos que possam ser explorados para fazer melhores previsões. A presença de autocorrelação nos resíduos pode indicar que a regressão não está capturando completamente a estrutura dos dados e pode levar a conclusões equivocadas.
4. Normalidade dos Resíduos: A regressão linear assume que os resíduos seguem uma distribuição normal. Em um modelo válido, os resíduos devem se aproximar de uma distribuição simétrica em torno de zero. Desvios significativos da normalidade podem afetar as propriedades estatísticas dos testes de significância e intervalos de confiança, prejudicando a precisão das inferências.
5. Ausência de Multicolinearidade: A multicolinearidade ocorre quando duas ou mais variáveis independentes estão altamente correlacionadas entre si. Isso pode causar problemas na interpretação dos coeficientes angulares, tornando difícil determinar a contribuição individual de cada variável independente para a variável dependente. Além disso, a multicolinearidade pode levar a estimativas imprecisas dos coeficientes e aumentar a variância das estimativas.
É essencial avaliar esses pressupostos antes de usar a regressão linear para análise. Uma maneira de fazer isso é por meio de gráficos de resíduos, testes estatísticos específicos e análise de resíduos. Se algum pressuposto não for atendido, é necessário tomar medidas corretivas, como transformar as variáveis, usar outras técnicas de modelagem ou até mesmo reconsiderar o uso da regressão linear para o conjunto de dados em questão.
Como realizar uma regressão linear
Para realizar uma regressão linear, é necessário seguir alguns passos fundamentais que nos permitirão encontrar a melhor linha de ajuste para os nossos dados. Vamos explorar o processo passo a passo:
1. Coleta e Preparação dos Dados: O primeiro passo é coletar os dados relevantes para as variáveis que desejamos analisar. Esses dados podem ser obtidos por meio de pesquisas, experimentos ou fontes confiáveis de dados disponíveis publicamente. É importante garantir que os dados estejam limpos, livres de erros e formatados corretamente para a análise.
2. Definir a Variável Dependente e as Variáveis Independentes: Em seguida, é necessário identificar a variável dependente (Y) que queremos prever ou explicar e as variáveis independentes (X) que serão usadas para fazer a previsão. Se for uma regressão linear simples, teremos apenas uma variável independente. Já na regressão linear múltipla, haverá duas ou mais variáveis independentes.
3. Plotar os Dados: Antes de realizar a regressão linear, é sempre útil plotar os dados em um gráfico para visualizar a relação entre as variáveis. Se for uma regressão linear simples, os dados devem formar uma dispersão ao longo de uma linha aproximadamente reta. Para a regressão linear múltipla, o gráfico de dispersão pode ser mais complexo, mas ainda buscamos padrões que possam ser representados por uma superfície linear.
4. Estimar os Coeficientes: O próximo passo é estimar os coeficientes da regressão linear. Na regressão linear simples, isso envolve determinar os valores de β₀ (coeficiente de intercepção) e β₁ (coeficiente angular) na equação Y = β₀ + β₁X + ε. Na regressão linear múltipla, precisamos encontrar os valores de β₀, β₁, β₂, …, βₚ, onde p é o número de variáveis independentes.
5. Método dos Mínimos Quadrados: A técnica mais comum para estimar os coeficientes é o método dos mínimos quadrados. Esse método busca minimizar a soma dos quadrados das diferenças entre os valores reais e os valores previstos pela equação da regressão. Os coeficientes ótimos são aqueles que melhor ajustam a linha de regressão aos dados disponíveis.
6. Interpretação dos Coeficientes: Uma vez que os coeficientes foram estimados, podemos interpretar seus valores para entender a relação entre as variáveis. O coeficiente de intercepção (β₀) representa o valor da variável dependente quando todas as variáveis independentes são iguais a zero. Os coeficientes angulares (β₁, β₂, …, βₚ) indicam como a variável dependente muda em resposta a uma mudança unitária nas variáveis independentes.
7. Avaliação da Qualidade do Modelo: Avaliar a qualidade do modelo é fundamental para garantir que a regressão linear seja adequada aos dados. Podemos usar métricas como o R-quadrado (R²) para medir o quão bem o modelo se ajusta aos dados. Quanto mais próximo de 1 o valor de R², melhor é o ajuste do modelo aos dados observados.
8. Análise de Resíduos: Por fim, é importante realizar uma análise de resíduos para verificar se os pressupostos da regressão linear foram atendidos. Isso inclui verificar se os resíduos estão distribuídos de forma aleatória em torno de zero, se a variância dos resíduos é constante e se não há correlação entre os resíduos.
Avaliação da qualidade do modelo
A avaliação da qualidade do modelo de regressão linear é uma etapa crucial para garantir que os resultados sejam confiáveis e úteis na análise de dados. Através dessa avaliação, podemos determinar o quão bem o modelo se ajusta aos dados observados e medir sua capacidade de fazer previsões precisas. Vamos explorar as principais métricas e técnicas utilizadas para avaliar a qualidade de um modelo de regressão linear.
1. R-quadrado (R²): O R-quadrado, também conhecido como coeficiente de determinação, é uma das métricas mais comuns para avaliar a qualidade do modelo. Ele varia de 0 a 1 e indica a proporção da variância total da variável dependente que é explicada pelas variáveis independentes incluídas no modelo. Quanto mais próximo de 1 o valor de R², melhor o ajuste do modelo aos dados. No entanto, é importante observar que um alto R² não necessariamente significa que o modelo seja adequado, pois pode estar sofrendo de overfitting, ou seja, ajustando-se muito bem aos dados de treinamento, mas com pouca capacidade de generalização para novos dados.
2. Coeficiente de Determinação Ajustado (R² ajustado): O R² ajustado é uma modificação do R² que leva em consideração o número de variáveis independentes no modelo e penaliza o acréscimo de variáveis desnecessárias que não contribuem significativamente para a explicação da variabilidade da variável dependente. O R² ajustado é especialmente útil quando comparamos diferentes modelos, permitindo-nos escolher aquele que melhor se ajusta aos dados, sem cair no problema do overfitting.
3. Erro Padrão da Estimativa (S.E.E.): O erro padrão da estimativa é uma medida de dispersão dos resíduos em relação à linha de regressão. Ele indica a magnitude média dos desvios entre os valores reais e os valores previstos pelo modelo. Quanto menor o S.E.E., melhor o ajuste do modelo aos dados e menor a dispersão dos resíduos.
4. Testes de Significância dos Coeficientes: Os testes de significância dos coeficientes são realizados para determinar se os coeficientes estimados são estatisticamente significativos. Em outras palavras, verificamos se as variáveis independentes têm uma influência significativa sobre a variável dependente. Os testes t ou testes F são comumente utilizados para essa finalidade.
5. Análise de Resíduos: A análise de resíduos é uma etapa crítica na avaliação da qualidade do modelo de regressão linear. Consiste em verificar se os pressupostos da regressão linear estão sendo atendidos. Os resíduos devem estar distribuídos de forma aleatória em torno de zero, a variância dos resíduos deve ser constante (homoscedasticidade), e não deve haver correlação entre os resíduos.
6. Validação Cruzada: A validação cruzada é uma técnica usada para estimar a capacidade de generalização do modelo. Ela envolve dividir o conjunto de dados em subconjuntos de treinamento e teste. O modelo é treinado nos dados de treinamento e avaliado em dados de teste independentes. Isso ajuda a evitar o overfitting e nos dá uma estimativa mais realista do desempenho do modelo em novos dados.
Limitações da regressão linear
1. Pressupostos Rígidos: A regressão linear tem certos pressupostos que devem ser atendidos para que os resultados sejam válidos. Esses pressupostos incluem a linearidade da relação entre as variáveis, a independência dos erros, a homoscedasticidade e a normalidade dos resíduos. Se algum desses pressupostos for violado, os resultados da regressão podem ser tendenciosos e imprecisos.
2. Sensibilidade a Outliers: Outliers, que são valores extremos que se desviam significativamente do padrão dos demais dados, podem ter um impacto substancial nos resultados da regressão linear. Eles podem distorcer a linha de ajuste e afetar os coeficientes angulares, tornando a regressão linear sensível a esses valores discrepantes.
3. Relações Não Lineares: A regressão linear assume uma relação linear entre as variáveis, o que pode ser uma simplificação excessiva em alguns casos. Se a relação entre as variáveis for curvilínea, uma regressão linear pode não ser capaz de capturar essa complexidade e levar a ajustes inadequados.
4. Multicolinearidade: A multicolinearidade ocorre quando duas ou mais variáveis independentes estão altamente correlacionadas entre si. Isso pode levar a estimativas imprecisas dos coeficientes angulares e dificultar a interpretação individual da influência de cada variável no modelo.
5. Extrapolação: A regressão linear é uma técnica de modelagem que faz previsões com base nos valores das variáveis independentes observados nos dados de treinamento. No entanto, ela não é adequada para fazer previsões fora da faixa de valores conhecida das variáveis independentes, ou seja, não é recomendado extrapolar além do intervalo de dados utilizados na construção do modelo.
6. Correlação não Implica Causalidade: Embora a regressão linear possa mostrar uma relação estatisticamente significativa entre variáveis, não significa necessariamente que uma variável cause diretamente a outra. A correlação entre duas variáveis não implica causalidade e outras variáveis não consideradas podem estar influenciando o relacionamento observado.
7. Overfitting e Underfitting: Overfitting ocorre quando o modelo se ajusta muito bem aos dados de treinamento, mas não consegue generalizar adequadamente para novos dados. Já o underfitting acontece quando o modelo é muito simples para capturar a complexidade dos dados. Ambos os problemas podem comprometer a capacidade do modelo de fazer previsões precisas.
Aplicações da regressão linear
Essas são apenas algumas das inúmeras aplicações da regressão linear em diversas áreas.
1. Economia e Finanças: Na área de economia e finanças, a regressão linear é amplamente utilizada para modelar relações entre variáveis macroeconômicas, como o PIB e a taxa de desemprego, ou variáveis financeiras, como o preço de ações e índices de mercado. Ela é útil para prever tendências econômicas, analisar impactos de políticas econômicas e avaliar riscos e retornos financeiros.
2. Ciências Sociais: Em ciências sociais, a regressão linear é aplicada para analisar o relacionamento entre variáveis sociais, como a renda e a educação, a satisfação do cliente em relação a um produto ou serviço e o impacto de campanhas de marketing ou políticas públicas em determinados comportamentos.
3. Ciências da Saúde: A regressão linear é amplamente utilizada em ciências da saúde para entender a relação entre variáveis biomédicas, como a dosagem de um medicamento e a resposta clínica de um paciente, a correlação entre fatores de risco e incidência de doenças e para prever resultados médicos, como a evolução de uma doença ao longo do tempo.
4. Engenharia e Tecnologia: Engenheiros e profissionais de tecnologia usam a regressão linear para modelar relações entre variáveis técnicas, como a relação entre a temperatura de um forno e a taxa de produção, o consumo de energia de um dispositivo eletrônico em relação à carga de trabalho ou a relação entre variáveis físicas e mecânicas de um material.
5. Pesquisa de Mercado e Análise de Dados Empresariais: Em pesquisa de mercado e análise de dados empresariais, a regressão linear é aplicada para entender como as variáveis de marketing (como preço, promoção, etc.) influenciam nas vendas de um produto, identificar fatores que afetam a satisfação do cliente ou analisar a relação entre despesas de marketing e receita de uma empresa.
6. Previsões e Planejamento: A regressão linear é amplamente usada em previsões e planejamento, desde prever a demanda futura de um produto com base em suas vendas passadas até fazer previsões econômicas e planejar orçamentos e recursos em empresas e organizações.
7. Análise de Dados Ambientais e Climáticos: Na área ambiental, a regressão linear é usada para entender o impacto das mudanças climáticas em variáveis ambientais, como a relação entre temperatura média e o derretimento de geleiras, ou a correlação entre níveis de poluentes e saúde pública.
Dicas práticas
A regressão linear é uma ferramenta poderosa para modelar relações entre variáveis e fazer previsões com base em dados. Para aproveitar ao máximo essa técnica, é importante seguir algumas dicas práticas que podem melhorar a qualidade da análise e garantir resultados mais robustos. Aqui estão algumas orientações úteis para utilizar a regressão linear de forma eficaz:
1. Entenda o Contexto e as Variáveis: Antes de iniciar a análise, é essencial entender o contexto do problema e as variáveis envolvidas. Defina claramente a variável dependente que deseja prever ou explicar, bem como as variáveis independentes relevantes que podem influenciar a variável dependente.
2. Verifique os Pressupostos da Regressão Linear: Antes de aplicar a regressão linear, verifique se os pressupostos da técnica estão sendo atendidos. Faça análises de resíduos, verifique a linearidade e a homoscedasticidade dos dados, bem como a independência dos erros. Se necessário, faça transformações nas variáveis para atender aos pressupostos.
3. Elimine Dados Ausentes ou Outliers: Dados ausentes ou outliers podem afetar significativamente os resultados da regressão linear. Se possível, tente eliminar dados ausentes ou aplicar técnicas de imputação para preenchê-los. Além disso, considere remover outliers se eles estiverem comprometendo a qualidade da análise.
4. Use Variáveis Adequadas: Selecione as variáveis independentes adequadas para a análise. Evite incluir variáveis altamente correlacionadas (multicolinearidade) e considere utilizar variáveis que tenham uma relação teórica ou lógica com a variável dependente.
5. Atenção ao Overfitting: Evite o overfitting, que ocorre quando o modelo se ajusta muito bem aos dados de treinamento, mas tem baixa capacidade de generalização para novos dados. Utilize técnicas de validação cruzada para avaliar a capacidade de generalização do modelo.
6. Interprete os Coeficientes com Cuidado: Ao interpretar os coeficientes de regressão, tenha cuidado para não tirar conclusões errôneas. Lembre-se de que correlação não implica causalidade e que a influência de uma variável pode ser mediada por outras variáveis não consideradas no modelo.
7. Considere Regressão Não Linear: Se a relação entre as variáveis não for linear, considere utilizar técnicas de regressão não linear, como regressão polinomial ou modelos baseados em curvas.
8. Atualize o Modelo Regularmente: À medida que novos dados são coletados, é importante atualizar o modelo de regressão regularmente para garantir que ele esteja refletindo a realidade atual.
9. Utilize Software Estatístico Confiável: Utilize software estatístico confiável e atualizado para realizar a análise de regressão. Isso garante resultados precisos e facilita a implementação das técnicas necessárias.
Seguindo essas dicas práticas, você estará preparado para utilizar a regressão linear de forma mais eficiente e obter insights valiosos a partir dos dados disponíveis. Lembre-se de que a análise de regressão é uma habilidade que pode ser aprimorada com a prática, e estar ciente das limitações da técnica é fundamental para realizar análises estatísticas sólidas e confiáveis.
Exemplo com Python
Passo 1: Dados
Vamos criar um exemplo de regressão linear utilizando Python para modelar a relação entre o número de horas de estudo por dia e o desempenho em uma prova. Suponha que temos os seguintes dados:
Horas de Estudo (X): [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Desempenho na Prova (Y): [50, 60, 70, 75, 80, 85, 90, 95, 100, 105]
Neste exemplo, queremos prever o desempenho na prova com base no número de horas de estudo por dia.
Passo 2: Importar as Bibliotecas
Primeiro, importamos as bibliotecas necessárias: NumPy para manipulação de dados numéricos e matplotlib para visualização dos gráficos.
import numpy as np
import matplotlib.pyplot as plt
Passo 3: Definir os Dados
Em seguida, definimos os dados de horas de estudo (variável independente X) e o desempenho na prova (variável dependente Y).
horas_estudo = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10])
desempenho_prova = np.array([50, 60, 70, 75, 80, 85, 90, 95, 100, 105])
Passo 4: Plotar os Dados
Vamos plotar os pontos de dados em um gráfico de dispersão para visualizar a relação entre as variáveis.
plt.scatter(horas_estudo, desempenho_prova)
plt.xlabel('Horas de Estudo por Dia')
plt.ylabel('Desempenho na Prova')
plt.title('Relação entre Horas de Estudo e Desempenho na Prova')
plt.grid(True)
plt.show()
O que resultará em:
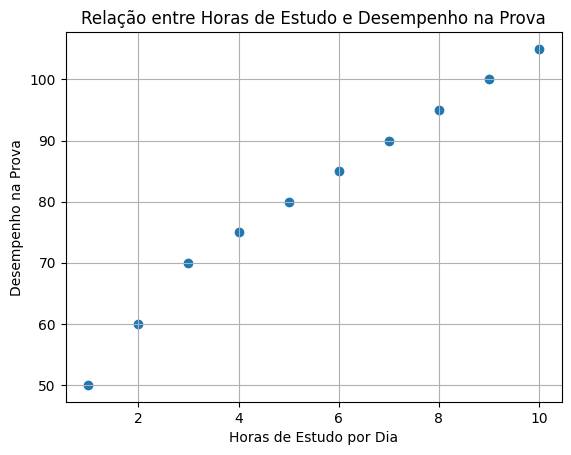
Passo 5: Realizar a Regressão Linear
Agora, vamos realizar a regressão linear para modelar a relação entre as variáveis.
# Adicionar uma coluna de 1s para o termo de intercepção (β₀)
X = np.column_stack((np.ones_like(horas_estudo), horas_estudo))
# Calcular os coeficientes da regressão linear
coeficientes = np.linalg.inv(X.T @ X) @ X.T @ desempenho_prova
# Coeficiente de intercepção (β₀) e coeficiente angular (β₁)
intercepcao = coeficientes[0]
coef_angular = coeficientes[1]
print("Coeficiente de Intercepção (β₀):", intercepcao)
print("Coeficiente Angular (β₁):", coef_angular)
O que resultará em:

Interpretação dos Coeficientes
Os valores fornecidos representam os coeficientes de uma equação linear na forma y = β₀ + β₁.x, onde “y” é a variável dependente e “x” é a variável independente.
Coeficiente de Intercepção (β₀): O coeficiente de intercepção, representado por β₀, é o valor no qual a reta da equação linear cruza o eixo vertical (eixo y) quando x é igual a zero. No contexto da equação y = β₀ + β₁.x, o valor β₀ é aproximadamente 49.33333333333336. Isso significa que quando x é igual a zero, o valor de y é aproximadamente 49.33333333333336.
Coeficiente Angular (β₁): O coeficiente angular, representado por β₁, é o valor que representa a inclinação da reta da equação linear. Ele mostra a taxa de mudança em y em relação a uma unidade de mudança em x. No contexto da equação y = β₀ + β₁.x, o valor β₁ é aproximadamente 5.7575757575757605. Isso significa que, para cada aumento de uma unidade em x, o valor de y aumentará em aproximadamente 5.7575757575757605.
A equação linear pode ser utilizada para fazer previsões ou estimativas quando um valor específico de x é conhecido. Por exemplo, para encontrar o valor estimado de y quando x é igual a 10, você pode substituir o valor de x na equação:
y = 49.33333333333336 + 5.7575757575757605 * 10
y ≈ 49.33333333333336 + 57.575757575757605
y ≈ 106.90909090909097
Portanto, quando estudarmos por 10 h (x), esperamos um resultado na prova aproximadamente 106.90909090909097 (y).
Passo 6: Plotar a Linha de Regressão
Vamos plotar a linha de regressão sobre os dados para visualizar o ajuste do modelo.
plt.scatter(horas_estudo, desempenho_prova)
plt.plot(horas_estudo, intercepcao + coef_angular * horas_estudo, color='red', label='Regressão Linear')
plt.xlabel('Horas de Estudo por Dia')
plt.ylabel('Desempenho na Prova')
plt.title('Relação entre Horas de Estudo e Desempenho na Prova')
plt.legend()
plt.grid(True)
plt.show()
O que resultará em:
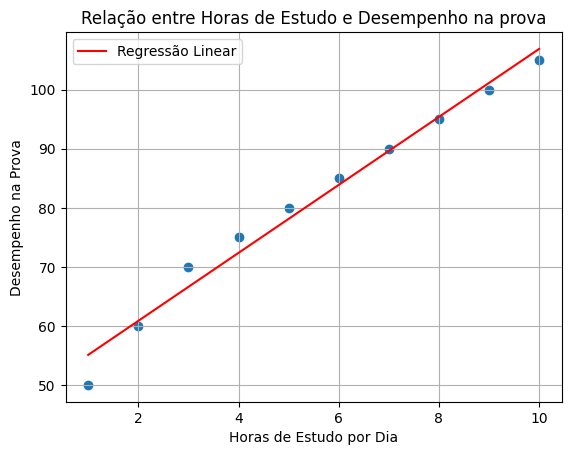
Resultado
O gráfico plotado mostrará os pontos de dados em azul (representando as horas de estudo e o desempenho na prova) e a linha de regressão em vermelho, que representa o ajuste do modelo. A inclinação da linha de regressão indica a relação entre as variáveis e o ponto em que a linha intercepta o eixo y representa o valor previsto quando as horas de estudo são igual a zero.
Esse exemplo de regressão linear nos ajuda a entender como podemos aplicar essa técnica para modelar relações entre variáveis e fazer previsões com base em dados. Lembrando que, em problemas reais, os dados podem ser mais complexos e será necessário ajustar o modelo adequadamente, mas a estrutura básica do processo de regressão linear é bastante semelhante.
Baixe o notebook do projeto
Para ver e/ou baixar o notebook do projeto, basta clicar no botão ao lado → → → →