Como referenciar este texto: Explorando a Análise Dimensional na Física: Compreendendo as Relações entre Grandezas. Rodrigo Terra. Publicado em: 22/11/2023. Link da postagem: https://www.makerzine.com.br/fisica/analise-dimensional-bl-002-aula-0010 .
Conteúdos dessa postagem
A análise dimensional é uma ferramenta essencial na física que nos permite compreender as relações entre diferentes grandezas e verificar a consistência das equações. É como um quebra-cabeça fascinante que nos ajuda a garantir que as peças se encaixem perfeitamente.
Entendendo a Análise Dimensional
No mundo da física, as grandezas são representadas por unidades de medida, como metros para comprimento, segundos para tempo e quilogramas para massa. A análise dimensional ajuda a verificar se as equações e fórmulas que usamos para descrever fenômenos físicos estão corretas e consistentes em termos de unidades.
Por exemplo, ao considerarmos a fórmula para calcular distância (d) utilizando velocidade (v) e tempo (t) (d=v×t), podemos aplicar a análise dimensional para confirmar sua validade:
- A unidade de velocidade é metros por segundo (m/s) e a unidade de tempo é segundos (s).
- Multiplicando a velocidade pelo tempo, obtemos (m/s)×(s).
- As unidades de tempo se cancelam, restando apenas a unidade de distância, que é em metros (m). Isso confirma que a equação está correta.

Aplicações da Análise Dimensional
Exemplo 1: Fórmula de Área
Ao calcular a área (A) de um retângulo usando comprimento (L) e largura (C) (A=L×C), a análise dimensional mostra:
- Área é medida em metros quadrados (m²).
- Comprimento e largura são medidos em metros (m).
- L×C resulta em metros×metros, o que é igual a metros2, a unidade correta para a área.
Exemplo 2: Lei de Newton
A segunda lei de Newton (F=m×a) relaciona força (F), massa (m) e aceleração (a):
- A força é medida em newtons (N).
- A massa é medida em quilogramas (kg).
- A aceleração é medida em metros por segundo ao quadrado (m/s²).
- Multiplicando massa pela aceleração, obtemos kg×m/s2, que é igual a N, confirmando a validade da equação.
Exemplo 3: Movimento de um Pêndulo
A equação para o período (T) do movimento de um pêndulo:
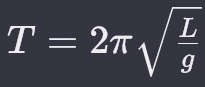
envolve o comprimento (L) do pêndulo e a aceleração devido à gravidade (g):
- O período é medido em segundos (s).
- O comprimento é medido em metros (m).
- A aceleração devido à gravidade é medida em metros por segundo ao quadrado (m/s²).
- A análise dimensional mostra que as unidades de T resultam em segundos, confirmando a validade da equação do pêndulo.
Fechamento
A análise dimensional é uma ferramenta poderosa na física, ajudando a verificar e validar as equações e relações entre as grandezas físicas. Essa técnica nos permite não apenas garantir a precisão das fórmulas, mas também compreender a consistência entre as unidades de medida, fornecendo uma base sólida para o entendimento dos fenômenos físicos.
Ao explorar e compreender a análise dimensional, podemos aprofundar nosso conhecimento sobre o mundo ao nosso redor e suas leis fundamentais.






